プロスペクト理論とは、利益や損失に関わる意思決定のメカニズムをモデル化した、行動経済学の理論です。
A案とB案のどちらを選ぶか、宝くじを買うかどうかなど、私たちは普段から多くの意思決定を行なっています。意思決定のプロセスを理解できれば、顧客などの心理を把握し、動かすのに役立つはずです。
今回は、プロスペクト理論の概要をわかりやすく説明したうえで、セールスや交渉、マーケティングでの活用法をご紹介します。
- プロスペクト理論とは
- プロスペクト理論の例
- プロスペクト理論の柱1：価値関数
- プロスペクト理論の柱2：確率加重関数
- プロスペクト理論から学べる5つのこと
- プロスペクト理論の活用例
- プロスペクト理論を学べる本
プロスペクト理論とは
プロスペクト理論とは、ダニエル・カーネマン氏とエイモス・トベルスキー氏が1979年に発表した、行動経済学の学説です。「価値関数」と「確立加重関数」を理論の柱とし、意思決定の場面で損得勘定がどう働くかを説明しています。prospectは、「（よいことが起こる）見通し」という意味です。
私たちの意思決定は、必ずしも合理的に行なわれているのではなく、感情や感覚による「ゆがみ」を伴っています。わかりやすい例が、宝くじです。
1等の当選確率は2,000万分の1という天文学的な数字（※）なのですが、なぜか私たちは、「ひょっとしたら当たるかも」と無謀な期待をしてしまいます。もし、人間がコンピューターのように合理的な思考をもっていたら、宝くじを買う人などいないかもしれません（※2018年の「年末ジャンボ宝くじ」1等の場合。0.00000005％）。
私たちは、物事が起こる確率を正確に認識しているわけではありません。小さな確率ほど大きく見積り、大きな確率ほど小さく見積ってしまうという、認知のゆがみをもっています。宝くじが当たる確率など皆無に等しいにもかかわらず、「ひょっとしたら当たるかも」という過度な期待を寄せてしまうのです。
従来の経済学では、「人間は常に合理的な意思決定をする」ことが前提だったため、実際の人間の行動パターンを十全に説明しきれず、理論と現実のあいだにズレが生じていました。そんななか登場したプロスペクト理論は、意思決定の不合理さを徹底的に観察して構築された、より現実に即した理論なのです。
プロスペクト理論の例
プロスペクト理論を解説する前に、意思決定における「不合理さ」を体感できる思考実験をご紹介しましょう。次章につながる内容も含んでいるので、読み飛ばさずにお付き合い下さい。なお、本章の記述は、経済学者の小川一仁氏らによる『実験ミクロ経済学』（東洋経済新報社、2012年）に基づいています。
賞金がもらえるくじ
あなたの前に、「くじA」「くじB」という2種類のくじがあるとします。どちらのくじを、より「欲しい」と思うでしょうか？
【Q1】
- くじA：100％の確率で4,000円をもらえる
- くじB：80％の確率で5,000円をもらえるが、20％の確率でハズレ（0円）。
「くじA」を選べば、必ず4,000円が手に入ります。対して「くじB」は、20％の確率で外れるものの、もし当たれば「くじA」よりも1,000円多くもらうことができる。
さて、あなたはどちらを選びましたか？ おそらく、よほどのギャンブラー気質でないかぎり、ハズレのない「くじA」を選んだのではないでしょうか。
このクイズの不思議なところは、「くじA」と「くじB」の期待値が同じであるにもかかわらず、なぜか「くじA」を選びたくなってしまう点。期待値というのは、くじやギャンブルにおける「賞金額の平均」を表す値で、「報酬×確率」の式で求められます。
- 「くじA」の期待値：4,000円×1＝4,000円
- 「くじB」の期待値：5,000円×0.8＋0円×0.2＝4,000円
どちらのくじも、期待値は4,000円。つまり、確率論的に考えれば、どちらのくじを引いても一緒のはず。
にもかかわらず、実際の心理としては、「くじAがいいな」となぜか感じてしまう。この矛盾は、なぜ生じるのでしょうか？ これが、プロスペクト理論以前の経済学では説明できなかった、1つ目の疑問です（疑問1）。
罰金を払わされるくじ
別のくじについても考えてみましょう。再び、「自分ならどちらのくじを選ぶか？」と考えながら読み進めてください。
【Q2】
- くじA：100％の確率で4,000円の罰金を支払う
- くじB：80％の確率で5,000円の罰金を支払うが、20％の確率で罰金なし
「くじA」を選ぶと、必ず4,000円の罰金を払わなくてはなりません。一方、「くじB」では、高確率で5,000円の罰金を支払うリスクがある代わりに、20％のアタリを引けば、何も支払わなくてよくなります。
あなたなら、どちらを選択しますか？ おそらく【Q1】とは反対に、多くの人は「必ず4,000円支払うなんて馬鹿馬鹿しい。まだ20％のアタリがあるほうがマシだ」と考えて、アタリのある「くじB」を選んだはずです。
この【Q2】でも、【Q1】と同様の問いを立てることができます。「くじA」「くじB」の期待値は、どちらもマイナス4,000円。それなのに、どうして「くじB」のほうが良いと感じてしまうのでしょうか？（疑問2）
【Q1】と【Q2】を見比べると、もうひとつ疑問がわいてきます。賞金がもらえる【Q1】では、リスクのないくじAが、罰金が課される【Q2】では、リスクのあるくじBが好まれる傾向にありました。賞金と罰金の違いこそあれ、金額も確率も同条件なのに、なぜ【Q1】と【Q2】で結果が逆になるのでしょうか？（疑問3）
このように、私たちの意思決定は、論理的に分析してみると数々の矛盾をはらんでいます。つまり、私たちは確率や金額といった客観的数値だけから合理的に（コンピューターのように）判断しているのではなく、感情や感覚などのノイズによって、少なからぬ影響を受けているのです。
【「くじ問題」の疑問まとめ】
- 【Q1】について、くじAとくじBの期待値は同じなのに、なぜくじAを選びたくなるのか？
- 【Q2】について、くじAとくじBの期待値は同じなのに、なぜくじBを選びたくなるのか？
- 「賞金か罰金か」以外は同じなのに、【Q1】と【Q2】で選ばれるくじが反対になるのはなぜなのか？
【疑問1～3】の答えは、次章以降、プロスペクト理論について学びながら解説していきましょう。
プロスペクト理論の柱1：価値関数
本章からは、プロスペクト理論の内容に踏み込みます。
前章では、「私たちの意思決定は必ずしも合理的ではなく、非合理的な『ノイズ』の影響を受けている」とわかりましたね。プロスペクト理論は、意思決定をゆがませる「ノイズ」を大きく2種類に分類します。「価値関数」と「確率加重関数」です。
専門用語が出てきましたが、決して難しい概念ではありません。一言でいえば……
- 価値関数：「価値の感じ方のゆがみ」を表すグラフ
- 確率加重関数：「確率の感じ方のゆがみ」を表すグラフ
「価値関数」と「確率加重関数」は、プロスペクト理論の2つの柱とされる重要な概念なので、しっかりと押さえておきましょう。
まず、柱の1つ目である「価値関数」を解説します。
「得」よりも「損」が重視される
「価値関数」とは、私たちの認知における「価値の感じ方の歪み」を表現する関数です。
私たちには、「得をした嬉しさよりも、損をしたガッカリ感を強く感じる」という心理傾向があります。たとえば、5万円をもらったときより、5万円をなくしたときのほうが、より大きく心が揺さぶられる感じがしませんか？ 5万円もらった嬉しさを「＋100」とするなら、5万円なくしたガッカリ感は「－200」くらい、という感じです。
要するに、同じ5万円という金額によってもたらされる価値（嬉しさやガッカリ感）は、金額に対して正比例ではありません。経済学者の筒井義郎氏らによる著書『行動経済学入門』（東洋経済新報社、2017年）によると、損失がもたらす影響は、利得のおよそ2.25倍だそう。プロスペクト理論における価値観数は、以下のようにグラフ化されます。
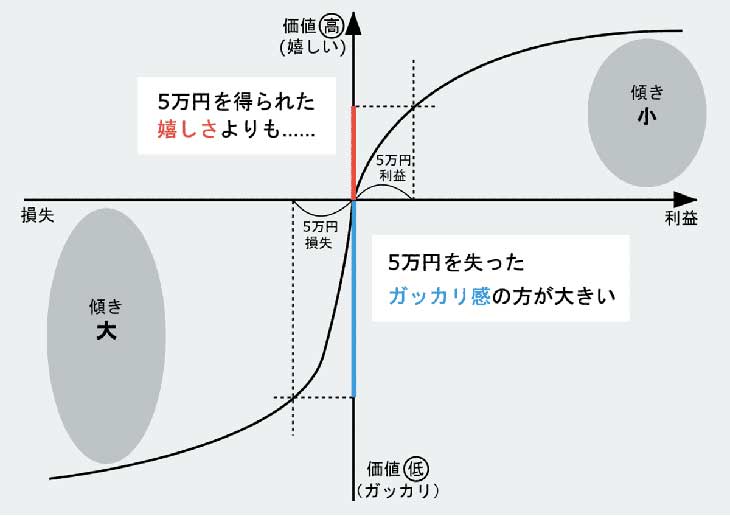
- 価値関数の横軸：利益・損失の金額
- 価値関数の縦軸：金額を得た／失ったことによる感情の大きさ
利益を得た場合（右半分）より、損をした場合（左半分）のほうが、グラフの傾斜が大きくなっているのがおわかりでしょうか。「得をした喜び」の幅より「損をしたガッカリ感」の幅のほうが大きい、ということが関数として表現されているのです。
感情は金額の大きさに比例しない
価値関数が直線ではなくS字カーブになっている原因は、「感応度逓減（かんのうどていげん）」。感応度逓減とは、利益・損失の額が大きくなっても、価値（喜びやガッカリ感）はあまり大きくならないという心理現象です。
たとえば、ギャンブルで「ゲームを始めてすぐに1万円勝った」ら、とても嬉しいはず。しかし、「100万円勝ったあとで、さらに1万円勝った」場合はどうでしょうか？ すでに手にした100万円によって、1万円の価値が薄まり、さほど嬉しく感じないはずです。
勝っていると安定志向、負けているとリスク志向になりやすい
ギャンブルや投資の経験がある人は、勝っているときほど慎重になり、負けているときほど大ばくちに出たくなったことがあるかもしれません。冷静に考えるなら、勝っているときは余裕があるのだから大きな勝負に出る一方、負けているときほど慎重になってもよさそうなもの。
しかし、実際の心理は逆に動くことが多いのです。下のグラフをご覧ください。
ギャンブルですでに10万円勝っている人は、さらに5万円勝つ場合の嬉しさよりも、5万円負けたときのガッカリ感を強く感じます。したがって、勝っているときは、「負けること」を強く避ける安定志向になるのです。
反対に、10万円負けているときには、さらに5万円負けるガッカリ感より、5万円取り返す喜びのほうが大きくなります。したがって、さらに負けるリスクを冒してでも、大きな賭けに出やすくなるのです。
「くじ問題」の分析
価値関数を使い、冒頭の「くじ問題」についても考えてみましょう。
「くじ問題」の【疑問1】は、「【Q1】について、くじAとくじBの期待値は同じなのに、なぜくじAを選びたくなるのか？」というものでした。「くじAとくじBの期待値は同じ」ということが前提でしたが、価値関数を使うと、別の見方ができます。
4,000円もらった嬉しさを、4,000joy（※）という単位で表してみましょう（※筆者が説明の便宜上つくった架空の単位）。では、5,000円もらった嬉しさは、5,000joyなのでしょうか？
しかし、価値関数においては、利益が大きくなるほどカーブは緩やかになります。そのため、5,000円もらったときの嬉しさは、5,000joyよりも少ない値、たとえば4,500joyくらいに減ってしまうのです。
4,000円もらった嬉しさを4,000joy、5,000円もらった嬉しさを4,500joyとして、期待値を計算し直してみましょう。
- くじA：100％の確率で4,000joyがもらえる
→4,000joy×1＝4,000joy - くじB：80％の確率で4,500joyがもらえる
→4,500joy×0.8＋0joy×0.2＝3,600joy
「くじA」の期待値のほうが大きくなりました。だから、私たちの心は「くじA」に動くのです。
【疑問2】も同様に解決できます。価値関数グラフの左半分に注目しましょう。4,000円の罰金を支払うガッカリ感を4,000sadとすると、5,000円の罰金を払うガッカリ感は、5,000sadよりも少ない値、たとえば4,500sadくらいになります。すると【Q1】同様、「くじA」のガッカリ感の期待値は4,000sad、くじBのガッカリ感の期待値は3,600sadになり、よりガッカリ感が少ない「くじB」が選ばれやすいのです。
そして、【疑問3】の「なぜ【Q1】と【Q2】では、選ばれるくじが反対になるのか？」については、「得をする場合（グラフの右半分）と損をする場合（グラフの左半分）で、カーブの向きが反対だから」と解答できます。このように、プロスペクト理論の柱のひとつ「価値関数」に着目すると、人間の意思決定プロセスが理解しやすいのです。
プロスペクト理論の柱2：確率加重関数
高い確率は低く、低い確率は高く感じられる
プロスペクト理論における2つ目の柱「確率加重関数」は、「確率の感じ方のゆがみ」を表現するグラフです。
「降水確率70％」「当選確率0.1％」など、確率は普段の生活でよく利用しますよね。しかし、私たちは、○○％と示された確率を客観的に理解しているわけではありません。人間には「高い確率ほど低く見積もり、低い確率ほど高く見積もる」という心理傾向があるのです。
「当たるはずのない宝くじをつい買ってしまう」のにも、確率加重関数が関係しています。私たちは、2,000万分の1（0.00000005％）という当選確率を正しく認識できず、実際よりも大きく見積る傾向があるので、「意外と当たるんじゃないか？」と感じてしまうのです。
反対に、大きな確率は実際よりも小さく感じられます。たとえば、「手術の成功率は99％です」と言われたら、ひょっとして失敗するんじゃないかと不安になってしまう人は多いのではないでしょうか。
このような「確率の感じ方のゆがみ」を表現したのが、確率加重関数です。『行動経済学入門』によると、確率加重関数では、およそ「40％」という値がターニングポイントなのだそう。つまり、約40％以下の確率は実際より高く感じられ、それ以上の確率は実際よりも低く感じられるのです（ただし、ターニングポイントは人によって異なります）。
「くじ問題」の分析
冒頭の「くじ問題」を、今度は確率加重関数を使って分析してみましょう。
【Q1】の「くじB」は、「80％の確率で5,000円がもらえるが、20％の確率でハズレ」という内容でした。確率加重関数に基づけば、5,000円がもらえる確率「80％」は実際より低く、ハズレの確率「20％」は実際より高く感じられます。したがって、「くじB」の感覚上の期待値は、実際の期待値である4,000円よりも低いのです。
一方、確率が100％の場合は、実際の確率と感覚とのズレが生じないので、「くじA」の期待値は4,000円のまま。したがって、「くじB」より「くじA」の期待値が高く感じられ、「くじA」を選びたくなるのです。
【Q2】においても、同様のメカニズムで、「くじB」より「くじA」の期待値が高く評価されます。【Q2】では、期待値が高いほうが罰金が多いので、【Q1】とは逆の「くじB」が好まれやすくなります。このように、「くじ問題」では、価値関数と確率加重関数によるバイアスが二重に作用していたのです。
価値関数や確率加重関数は、あくまで統計から導いた傾向です。よほどの安定志向の人や、リスク志向の人など、当てはまらない人もいることでしょう。とはいえ、人々のおおまかな心理傾向を知っておけば、プロスペクト理論は大いに役立ちます。
プロスペクト理論から学べる5つのこと
前章までの内容のまとめとして、プロスペクト理論のポイントを5つに要約しました。プロスペクト理論の全体像を整理するのに役立ててください。
プロスペクト理論の柱は「価値関数」と「確率加重関数」
価値関数とは「価値の感じ方のゆがみ」を表現するグラフ、確率加重関数とは「確率の感じ方のゆがみ」を表現するグラフでした。
損失のほうが価値づけが重い
金額が同じだと、損をした場合、得をした場合の約2.25倍の価値を感じます。そのため、私たちは、得をすることよりも損を避けることを優先する傾向があるのです。
金額が大きくなるほど、価値の感じ方は小さくなる
動く金額が大きくなるほど、もたらされる価値（得をした嬉しさ／損をしたガッカリ感）の振れ幅は小さくなっていきます。賞金が2倍になっても、嬉しさも2倍になるわけではないのです。
勝っているときは安定志向、負けているときはリスク志向
価値関数はS字カーブを描いています。利益が出ているときには安定志向になる一方、損害が出ているときは、リスクを冒してでも利益を目指す心理が働きやすくなるのです。
確率は正しく認識されない
私たちは、約40％よりも高い確率を実際より低く評価し、それよりも低い確率を実際より高く評価する傾向があります。その心理的傾向を表現したグラフが確率加重関数です。
プロスペクト理論から学べることはたくさんありますが、少なくとも上記の5ポイントは押さえておきましょう。
プロスペクト理論の活用例
プロスペクト理論は、ビジネスにおいてどのように活用できるのでしょうか。3つの例を紹介しましょう。
フィア・アピール
プロスペクト理論によると、私たちは利得よりも損失を重く評価する傾向があります。この損失回避性を応用したのが「フィア・アピール」です。
フィアとは英語で「恐怖」のこと。「この商品を買わないと損しますよ」というように、顧客が被る損失をアピールし、購買意欲を高めることを狙う交渉テクニックが、フィア・アピールです。たとえば、「この化粧品を使うと肌のハリが増します」と言うよりも、商品を使わないことによって失うものに着目し、「この化粧品の成分が不足すると、肌のハリがなくなりますよ」と宣伝します。
セールスコピーライターの大橋一慶氏は、フィア・アピールの例として、以下のものを紹介しています。
- 保険商品：「もしあなたが事故にあったら、家族はどうなるでしょうか？」
- 害虫駆除：「シロアリは、あなたの大切な家をボロボロにしてしまいます」
- 英会話教材：「間違った英語で、外国人を怒らせてしまっているかもしれません」
- 金融商品：「賢く資産運用をしないと、老後の貯えが心配です」
上記以外にも、フィア・アピールはさまざまな商品の宣伝に役立ちます。「数量限定」「期間限定」なども、フィア・アピールの一種。もちろん、いたずらに危機感をあおるのはよくありませんが、伝え方を工夫するだけで、商品の売れゆきを改善できるかもしれません。
リスクリバーサル
フィア・アピールとは反対に、顧客の不安を取り除くことで購入を促す技術が「リスクリバーサル（リスク保証）」です。私たちが商品を買おうとするときには、「買って損をしたらどうしよう」という不安がつきもの。せっかく商品に魅力を感じていても、不信感が拭いきれず、購入に踏み切れない顧客も少なくないはずです。
リスクリバーサルの例は、以下のようなもの。「商品を買って、もし失敗したと感じても大丈夫」と、顧客を安心させることが肝になります。
- 返金保証
- 分割払い
- カスタマーサポート
- 修理保証
心理学に詳しい起業家・宮川明氏らの著書『成約率が20倍になった「セールスレター」の秘密』（秀和システム、2006年）によると、実際の商品を確認できない通販では、リスクリバーサルが特に重要なのだそうです。
フレーミング効果
プロスペクト理論を情報伝達に応用したのが「フレーミング効果」です。フレーミング効果とは、表現方法（フレーム）が違えば、受け手に与える印象も変わるという心理効果。たとえば、「90％の顧客が店舗Aのリピーターになる」と「10％の顧客が二度と店舗Aを利用しない」とでは、意味こそ同じですが、まるきり違う印象を受けますよね。
SBI大学院大学でビジネス・ミクロ経済学などを教える石川秀樹氏は、フレーミング効果の影響力を実感できる思考実験を紹介しています。「600人中200人が確実に救われる政策A」と、「3分の1の確率で600人全員が助かり、3分の2の確率で誰も救われない政策B」は、どちらがよいでしょう？ 多くの人は、「600人中200人が確実に救われる政策A」を選ぶはずです。
では、質問の表現を反対にしてみましょう。「600人中400人が確実に死ぬ政策A」と、「3分の1の確率で誰も死なずに済み、3分の1の確率で600人全員が死亡する政策B」ではどちらがいいか？ 迷うところですが、「3分の1の確率で誰も死なずに済む政策B」を選ぶ人が多いのではないでしょうか。
表現が違うだけで、なぜ判断に影響が生じるのでしょう？ この疑問も、プロスペクト理論で説明できます。
ミソとなるのは、「価値関数」の項目で解説した「利益が出ている場合は安定志向になり、損失が出ている場合はリスク志向になる」という心理。つまり、利益に関わる情報においては「確実に○○できる」という確実性の高い表現が好まれ、反対に、損失に関わる情報においては「××％の確率で△△する」というリスク表現が好まれやすいのです。
「利益を伝えるなら確実表現、損失を伝えるならリスク表現」という簡単なルールを覚えておくだけで、顧客への商品説明や会議での報告などの際、きっと役に立つはず。プロスペクト理論とフレーミング効果を活用し、なるべく有利に話を運べるよう、賢く情報を伝えましょう。
プロスペクト理論を学べる本
最後に、プロスペクト理論についてもっと深く学びたい人向けに、本記事の参考資料としても活用した3冊の本をご紹介します。
『ケーススタディで学ぶ 入門 ミクロ経済学』
SBI大学院大学講師の石川秀樹氏による著書です。タイトルどおり、経済学の入門者向けに書かれているので、文章が簡明で読み進めやすいのが長所。カラーの図解が多く、抽象的な経済学の概念を視覚的にわかりやすく学べます。これから経済学やプロスペクト理論を学びたい方は、まず最初に手に取ってみてはいかがでしょうか。
『実験ミクロ経済学』
2冊目は、経済学者の小川一仁らによって著された『実験ミクロ経済学』。専門用語や数式がありながら、文章は易しいため、発展的な内容を学びたい方にオススメです。タイトルどおり、経済学の実験や思考実験についての記述が多いので、具体例に触れながら楽しく読み進めることができます。
『行動経済学入門』
3冊目は、経済学者の筒井義郎氏らによる『行動経済学入門』。行動経済学におけるほかの理論・知識とプロスペクト理論を関連づけ、体系的に学習できます。上記2冊と比べれば文章は堅いですが、行動経済学の実験例やグラフなどが多数載っているので、プロスペクト理論や行動経済学の初学者でも理解しやすいはずです。
＊＊＊
プロスペクト理論を理解しておくと、相手の意思決定をある程度コントロールし、ビジネスを有利に進めることに役立ちます。セールスや交渉事などに苦手意識がある方は、ぜひ本記事の内容を参考に、プロスペクト理論を活用してみてくださいね。
（参考）
小川一仁, 川越敏司, 佐々木俊一郎（2012）,『実験ミクロ経済学』, 東洋経済新報社.
筒井義郎, 佐々木俊一郎, 山根承子, グレッグ・マルデワ（2017）,『行動経済学入門』, 東洋経済新報社.
All About｜年末ジャンボ宝くじ2018の当せん確率とおすすめの買い方
コトバンク｜期待値
みんなのコピー｜フィア・アピール（恐怖アピール）の正しい使い方
宮川明, 濱田昇（2006）,『成約率が20倍になった「セールスレター」の秘密』, 秀和システム.
石川秀樹（2010）,『ケーススタディで学ぶ 入門 ミクロ経済学』, PHP研究所.
【ライタープロフィール】
佐藤舜
大学で哲学を専攻し、人文科学系の読書経験が豊富。特に心理学や脳科学分野での執筆を得意としており、200本以上の執筆実績をもつ。幅広いリサーチ経験から記憶術・文章術のノウハウを獲得。「読者の知的好奇心を刺激できるライター」をモットーに、教養を広げるよう努めている。
